Generating an icosphere with code (Archive)
⛔️ This page is an outdated version of a post that has been modified after its original publication. This version describes icosphere generation strategies that were further improved and it’s maintained for reference purposes only. You should read the revised post instead.
In this article, we will walk through the process of generating icospheres (spheres based on a regular icosahedron) with code. I started looking into icospheres when working on Terraced Terrain Generator (TTG) version 2, which added support for spherical terrains. I took some time to study different sphere types and ended up creating a small library to procedurally generate spheres (ico-, cube- and UV-spheres) in Unity: Sphere Generator. Building the library inspired me to write this piece.
The article’s content is divided into 5 sections. The first one introduces the concept and characteristics of the icosphere. The remaining sections correlate to the 4 generation steps. The conclusion wraps the article up.
The icosphere
Before jumping into details, it’s important to understand what an icosphere is. It’s uncertain (at least to me) who invented the term icosphere, but the most popular usage of the term is in the 3D modeling tool Blender, which defines the term as:
An icosphere is a polyhedral* sphere made up of triangles. Icospheres are normally used to achieve a more isotropical layout of vertices than a UV sphere, in other words, they are uniform in every direction.
*: A polyhedral shape is a shape that represents a polyhedron: a 3-dimensional shape with flat, polygonal faces. Pyramids and cubes are examples of polyhedrons.
The image below displays an example of an icosphere:

Characteristics
Multiple techniques can be used to generate spheres, and each one creates meshes with different properties. The icosphere has the following characteristics:
- Its triangles have about the same area.
- Its triangles are equilateral—or as close to it as possible.
- Its triangles are oriented non-uniformly. There are 20 areas (we will soon see why 20) with distinct triangle orientation. The image above displays a point on its center where five of these areas meet, forming a pentagon. Each one of the five triangles has a different orientation.
- It is uniform in every direction. It doesn’t matter which direction you move on an icosphere, the shape, area and consequently the concentration of triangles remains mostly unchanged. Therefore, it doesn’t have poles, unlike the UV sphere.
- Unlike UV spheres, it isn’t a great fit for texture mapping.
- It is a better fit when modeling more natural shapes.
The icosahedron
Knowing what an icosphere looks like is one thing. Knowing how to generate one is something completely different. In order to learn how to generate icosphere meshes procedurally, we need to understand the concepts behind it. First, how can we conceptually define an icosphere?
An icosphere is generated by fragmenting and normalizing a regular icosahedron.
Let’s break that sentence down. First, what on earth is an icosahedron, and what makes one regular?
An icosahedron is a polyhedron with 20 faces. There is an infinite number of icosahedrons, and the most famous one is the regular icosahedron, a convex polyhedron composed of 20 equilateral triangles. The regular icosahedron is one of the five Platonic solids and, for the RPG players out there, D20 dice are shaped like it. This is how it looks like:

The process described in this article creates an icosahedron (the rotating shape above) and transforms it into an icosphere. It consists of four steps:
- Icosahedron generation.
- Fragmentation.
- Normalization.
- Scaling.
The next sections describe the steps above in detail.
ℹ️ Even though an icosphere can be of any size, for the sake of comprehension, the next three sections describe the process of generating a unit icosphere: an icosphere with radius of 1.
Step 1: Icosahedron generation
First, it’s important to define what it means to generate a 3D shape. Traditionally, virtual 3D shapes are represented as meshes composed by simple primitives like squares or, more commonly, triangles. Regardless of how detailed, complex and large a 3D mesh is, it can be decomposed into small triangles. The larger the number of triangles, the more detailed a mesh can be and the more resources are needed to load and display it are necessary. Here’s an example of a 3D model of the famous Utah teapot with its mesh elements displayed:

Notice how the entire teapot is composed by triangles, regardless of how detailed the mesh area is. The areas which are less detailed—like the center of its side—have a smaller concentration of triangles. Highly detailed areas—like the lid’s knob—have a higher concentration of triangles.
Every triangle of a 3D mesh can be represented by the coordinate of its 3 vertices. Once we have that data, we can draw the triangle. To draw the entire 3D model, all we need is to repeat the drawing process on all triangles on the mesh. Therefore, in order to represent a 3D mesh, all we need is:
- The coordinates of all of the triangle vertices.
- Which vertices belong to each triangle. This is often referred to as “triangle indices”, where each vertex is represented by an index.
Generating an icosahedron is no different; all we need is its vertices and triangle indices. Finding the vertices coordinates is particularly interesting. Once you’ve got those, the triangle indices are easy to find.
There are different paths one can take to gather vertex data on a regular icosahedron. The path I took aims to find them by using mutually perpendicular rectangles of particular dimensions (more on this soon). The image below demonstrates an example of such rectangles, with each one colored differently to ease viewing:

The vertices of the triangles (highlighted with tiny pink balls) will become the vertices of the icosahedron. There are twelve of them, 4 for each rectangle. The white lines define 20 faces and are placed where the icosahedron’s edges would be. Contrast this image with the rotating icosahedron one in the previous section and the correlation becomes clear.
Finding the vertices
The first step to construct the rectangles is to find the coordinates of their 4 vertices. We know all rectangles are placed at the same point in space (i.e. their centers share the same coordinates), and we choose that point to be the origin: (0, 0, 0). We have also established that all rectangles have the same dimensions. Consequently, they only differ in rotation and, once we have found the coordinates of one rectangle’s vertices, we can just rotate them to find the coordinates of the other 2.
The rectangles can be of any size, as long as the ratio between their sides is the golden ratio, which is approximately 1.618033988749. Effectively, this means that the rectangle’s width must be ~1.618 times larger than its height. We also know that all rectangle vertices must be at 1 unit away from its center (it’s a unit sphere), so we can calculate the rectangle’s height and width based on the diagram below:
Where a is height/2 and c is width/2. The white rectangle above represents one of the 3 rectangles we are going to use to build the icosahedron. The circle is there merely to display all points that are placed 1 unit away from the rectangle’s center. The coordinates of all 4 rectangle vertices can be defined in terms of a and c on a (x,y) plane:
Therefore, in order to find the vertices coordinates, we need to find the values of a and c. We already have enough information to do so, since:
- The golden ratio determines that
width = height * goldenRatio, and thereforec = a * goldenRatio. - The
a/b/1triangle (represented by dotted lines in the first rectangle image) is equilateral, and therefore we can use Pythagoras’ Theorem.
With that in mind:
1
2
3
4
5
6
7
8
1² = a² + c² // Pythagoras' Theorem
1 = a² + (a * goldenRatio)² // c = a * goldenRatio, 1² = 1
1 = a² + a² * goldenRation² // Exponent distribution (power rule)
1 = a² * (1 + goldenRation²) // "a" is a common factor
a² = 1 / (1 + goldenRation²) // Divide both sides by a² and flip
a = √(1 / (1 + goldenRatio²)) // Apply square root on both sides
a = √(1 / (1 + 2.618033988749895)) // Replace golden ratio value
a = 0.525731112119134 // Solve the square root
Once we know that a = 0.525731112119134, finding c becomes trivial:
1
2
3
c = a * goldenRatio
c = 0.525731112119134 * 1.618033988749 // Replace values
c = 0.85065080835157
Now that we have the coordinates of the rectangle’s vertices, we can construct it using 2 triangles, like seen in the image below:
The first triangle is composed by vertices v0, v1 and v3 and the second one by vertices v1, v2 and v3. The vertices coordinates are, approximately:
-
v0: (-0.85, +0.52). -
v1: (+0.85, +0.52). -
v2: (+0.85, -0.52). -
v3: (-0.85, -0.52).
All of these vertices are 1 unit away from the rectangle’s center—in other words, their vector has length 1. As we have seen, once we have the vertices coordinates for one rectangle, we can just rotate them to find the vertices’ coordinates of the other 2 rectangles. The rotation process modifies a vector’s direction, but not its length. Therefore, all 12 vertices will have length 1.
With that, we have gathered all the vertex information we needed to construct the icosahedron.
Constructing the faces
Once the coordinates of all vertices are known, we need to find the triangle indices: the list of vertex indices that are used to create all the 20 triangles of the icosahedron. A unique index is assigned to each vertex, spanning from 0 to 11. The triangle indices list contains 60 elements—3 for each of the 20 triangles of the icosahedron. Each element is a vertex index in the [0, 11] range.
Creating this list is not as challenging as finding the vertex positions. In fact, I am not aware of a procedural method to assign the triangle indices (leave a comment if you know one!), and I found them by trial and error. Having a reference image (like the one with the 3 mutually perpendicular rectangles in the previous section) was extremely helpful. It sounds like a cumbersome task, but it didn’t take long (~15 minutes) and honestly, it was a nice exercise in mesh construction and I kind of enjoyed it. I probably wouldn’t think the same if the mesh had many more triangles, but an icosahedron was manageable.
If you would like to take a look at the triangle indices and the vertex coordinates I’ve found, take a look at Sphere Generator’s source code.
Step 2: Fragmentation
Step 1 leaves us with a regular icosahedron, a shape which lacks detail and doesn’t contain enough vertices to pass as a sphere. To remedy that, we need to generate more vertices; and that’s where mesh fragmentation comes in.
Mesh fragmentation is the process of procedurally increasing the vertex count of a mesh by fragmenting its primitives (in this case triangles) into new, smaller ones. It aims to allow the mesh to provide more detail than existing, without actually adding the detail information (that is step 3’s role).
Fragmenting a mesh composed only by triangles consists of turning each triangle into 4 smaller ones, while preserving the shape of the original. The image below displays an example of a triangle (larger, outer lines) that has been fragmented once into 4 smaller ones. It also happens to unequivocally resemble The Legend of Zelda’s triforce:
When it comes to an icosahedron, we need to keep in mind that the fragmentation process must not change the mesh’s topology. In this case, it is enough to ensure that all triangles in the mesh are equilateral. Luckily, equilateral triangles are particularly easy to fragment and the operation conserves equilaterality. The image above is also an example of the fragmentation of an equilateral triangle into 4 smaller, equally equilateral triangles.
ℹ️ Although this section uses C# as its guiding programming language, the code described here should be easily translatable to other programming languages.
Let’s look into how to fragment triangles with code. Like in every fragmentation process, the original vertices are maintained—failing to do so would change the mesh’s shape. Three new vertices are created by finding the mid-point of each edge. The coordinates (x, y, z) of a mid-point of an edge with vertices v1 and v2 can be calculated as:
1
2
3
var x = (v1.x + v2.x) / 2;
var y = (v1.y + v2.y) / 2;
var z = (v1.z + v2.z) / 2;
The fragmentation process can be repeated indefinitely. Each iteration increases the number of triangles by a multiplying factor of 3, bringing the total number of triangles to 4 times the original one (1 + 3). The total number of iterations is often referred to as fragmentation depth. The image below displays an example of a triangle that went through a fragmentation process with a depth of 2, resulting in 16 triangles (4²).
With this in mind, we can apply the fragmentation process to the regular icosahedron. The image below displays a regular icosahedron followed by three meshes that are the outcome of fragmenting it with a depth of 1, 2 and 3 respectively.

Notice how, although the number of triangles increased from 20 to 80, then to 320 and finally to 1280, the shape of the mesh hasn’t changed (if you struggle to see it, look at the contour). The original faces and edges are still untouched—they just have more vertices and triangles now. In other words, the meshes above are all icosahedrons; just with different triangle counts.
Step 3: Normalization
As we can see in the previous section, even though the number of triangles increases with every fragmentation iteration, the shape of the mesh remains unchanged. The cause is clear: during fragmentation, new triangle vertices are placed on the same plane as the triangle they originally belonged to. As a result, no new planes or faces are created. To address this issue, the new vertices need to be repositioned to “break out” of their plane, effectively changing the mesh’s shape in a manner that resembles a sphere. The question at hand is: how to do that?
Here’s where one of the sphere’s properties comes in handy: all points on the surface of a sphere are equally distant from its center, and that distance is called radius. In the case of a unit sphere, the radius is equal to 1. This property holds for all 12 original vertices of the icosahedron (as we demonstrated above), but it doesn’t for the new vertices—they are closer to the sphere’s center than the original ones. Logically, the next step would be to ensure that the radius property holds for all vertices by moving them away from the center. The question now is: in which direction should we move them?
To answer this question, we revisit the characteristics of the icosphere. We would like to, as much as possible, keep:
- All triangles close to an equilateral one.
- The area of all faces similar.
- The triangle distribution as uniform as possible.
A great way to closely maintain these properties is to normalize the vertices. Normalization is the process of converting a given vector into a unit vector: a vector with a length of 1. This operation modifies the length of the vector but keeps its direction unmodified. The image below displays how we can use vector normalization to ensure that a vertex respects the sphere radius property:
In the image, the circle represents a slice of the sphere passing through its center. The circle’s radius is 1. The surface of the icosahedron is represented as a square for simplicity’s sake. The distance between the square’s corners and the center of the circle is 1—just like the original vertices of the icosahedron are placed 1 unit away from the sphere’s center. Vertices v1 and v2 represent all “new” vertices: vertices that are not part of the original icosahedron and were generated by fragmentation. They are placed on the surface of the icosahedron and the distance between them and the center of the circle is less than 1.
In this case, vertices v1and v2 are normalized into vectors v1n and v2n, respectively. The normalization operation maintains their direction but “expands” them, ensuring that their length is equal to 1, effectively placing them on the sphere’s surface. Problem solved.
Now that we know how to reposition a vertex without deviating too much from the icosphere properties, we can apply normalization on all vertices:
1
2
3
4
5
6
7
8
void NormalizeAllVertices(Vector3[] vertices)
{
for (var index = 0; index < vertices.Length; index++)
{
var vertex = vertices[index];
vertices[index] = vertex.normalized;
}
}
Where vertex.normalized returns a normalized version of the given vertex. This operation is extremely common and is often included in game engine libraries (e.g. Vector3.normalized is defined in both Unity’s and Godot’s libraries). It is even present in some programming languages’ standard libraries, like C#’s.
The outcome of the normalization process can be observed in the image below. The first row is identical to the image at the end of the fragmentation section and contains icosahedrons that have not been normalized. The first mesh in that row is the regular icosahedron, followed by fragmented meshes with a depth of 1, 2 and 3 respectively. The bottom row displays the normalized version of the top row, keeping their fragmentation depths.


It’s worth noting that the number of vertices in the meshes on each column is identical; the only difference is the position of each of the mesh’s vertex. It is also clear that the higher the fragmentation depth, the closer to a continuous sphere the normalized meshes get—their contour progressively resembles a circle. Finally, it is evident that both steps are necessary: fragmenting without normalization increases detail but doesn’t change the mesh’s shape and normalization without fragmentation accomplishes nothing—all vertices of an icosahedron are already normalized.
The GIF below summarizes the process, composed by fragmentation and normalization (steps 2 and 3 respectively). It starts with a regular icosahedron which is fragmented twice (hence depth = 2). Then, the icosahedron is progressively (for educational purposes) normalized until all vertices are equally distant from the mesh’s center. The final mesh represents an icosphere.
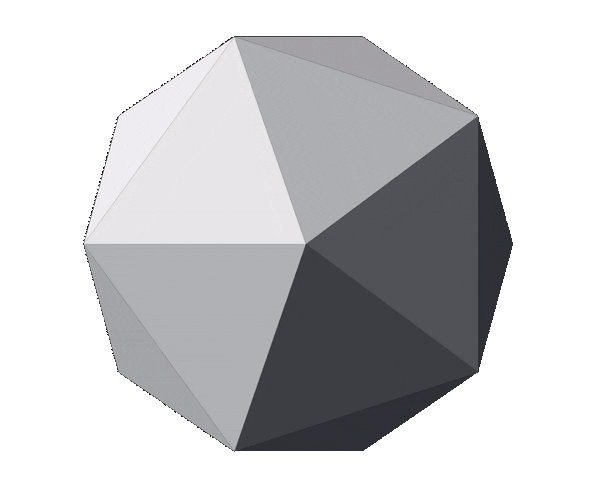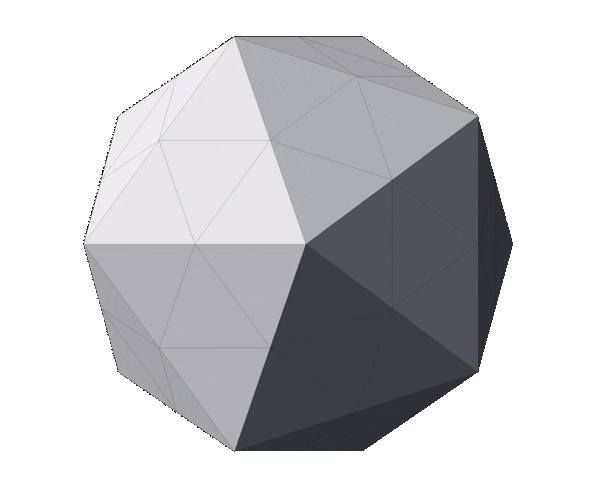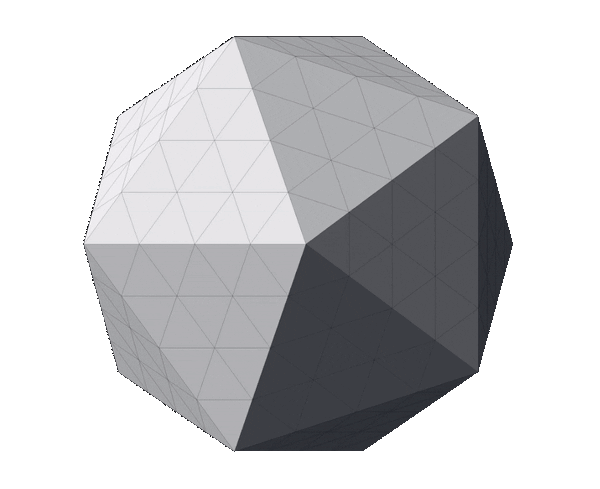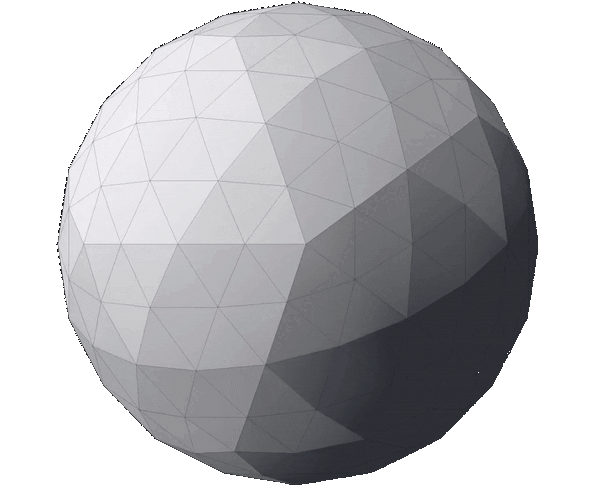
At this point, we have concluded the process of generating an icosphere. The next step, described below, is optional and it aims to scale the mesh to meet multiple purposes.
Step 4: Scaling
The previous generation steps left us with a unit icosphere. Even though that mesh is an icosphere, we would often like to easily tinker with sphere size. To accommodate for that, we can easily modify the NormalizeAllVertices method from step 3 to introduce a new parameter: the sphere’s radius:
1
2
3
4
5
6
7
8
void RepositionAllVertices(Vector3[] vertices, float radius)
{
for (var index = 0; index < vertices.Length; index++)
{
var vertex = vertices[index];
vertices[index] = vertex.normalized * radius;
}
}
With that, we can generate all icospheres one can imagine—as long as one’s computer can handle it.
Conclusion
In this article, we learned what an icosphere is, what its properties are and how we can generate one procedurally, using code. We also observed how the different generation steps influence the final mesh. Finally, we saw how the fragmentation depth impacts the mesh’s level of detail and, therefore, its similarity with real, continuous spheres.
The techniques described here were used to add spherical terrain support to Terraced Terrain Generator (TTG) version 2 and Sphere Generator’s icosphere support.
That’s a wrap! As usual, feel free to use the comment section below for questions, suggestions, corrections, or just to say “hi”. See you on the next one!
-
Previous
-
Next





